Problem One: FIR Design from
Ideal Filter
(40 points)
A Finite Impulse Response (FIR) filter is a
linear shift invariant filter whose impulse response function is a
finite-extent discrete signal. For an FIR filter, the output can be determined
from its input by means of the convolution sum, expressed as,
![]()
With support over the region, ![]() , where
, where ![]() .
.
1. Use the Image Processing
Toolbox of MATLAB to design a low-pass filter with a given characteristics
(defined by each student group). Provide a plot of, both, impulse response and
frequency response of the designed filter using a rectangular window.
2. Repeat part 1 above with
three different types of additional windows.
SOLUTION:
1)
Use the Image Processing Toolbox of
MATLAB to design a low-pass filter with a given characteristics (defined by
each student group). Provide a plot of, both, impulse response and frequency
response of the designed filter using a rectangular window.
The impulse response h(n) is obtained at the output when the
input signal is the impulse signal ![]() . The impulse
signal is defined by
. The impulse
signal is defined by
![$\displaystyle \delta(n)\isdef \left\{\begin{array}{ll}
1, & n=0 \\ [5pt]
0, & n\neq 0 \\
\end{array}\right..
$](FINAL_CAM_YYS_1_files/image009.gif)
If the ![]() th tap is
denoted bk,
then it is obvious that the impulse response signal is given by
th tap is
denoted bk,
then it is obvious that the impulse response signal is given by
![$\displaystyle h(n)\isdef \left\{\begin{array}{ll} 0, & n<0 \\ [5pt] b_n, & 0\leq n\leq M \\ [5pt] 0, & n> M \\ \end{array} \right. \protect$](FINAL_CAM_YYS_1_files/image011.gif)
In other words,
the impulse response simply consists of the tap coefficients, prepended and appended by zeros.
The original image:

1) For the characteristics defined as:
For a frequency space of 3
and a boxcar window of 3 the results are:
Plot of the frequency
response and the impulse response:
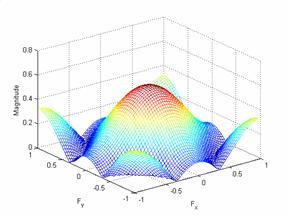
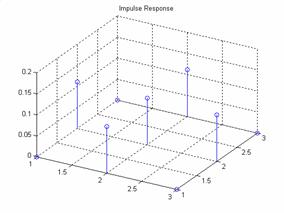
The output:

For a frequency space of 5
and a boxcar window of 5 the results are:
Plot of the frequency
response and the impulse response:
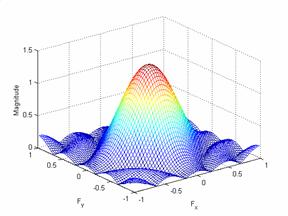
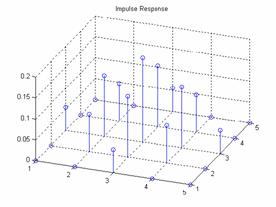
The output:

For a frequency space of 10
and a boxcar window of 10 the results are:
Plot of the frequency response
and the impulse response:
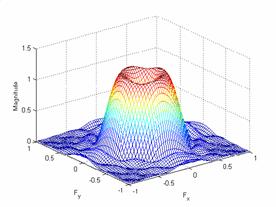
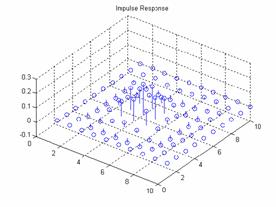
The output:

2) Repeat part 1 above with three different types of additional windows.
Hanning Window:
For a frequency space of 10
and a hanning window of 10 the results are:
Plot of the frequency
response and the impulse response:

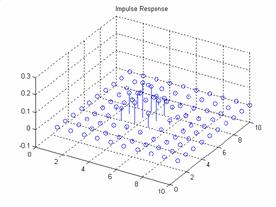
The output:

Hamming Window:
For a frequency space of 10
and a hamming window of 10 the results are:
Plot of the frequency
response and the impulse response:
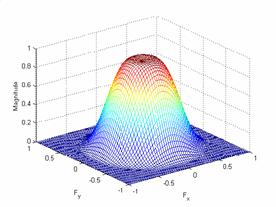
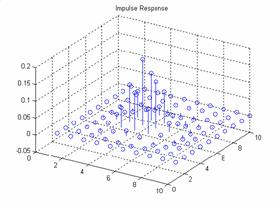
The output:

Blackman Window:
For a frequency space of 10
and a blackman window of 10 the results are:
Plot of the frequency
response and the impulse response:
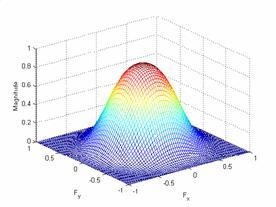
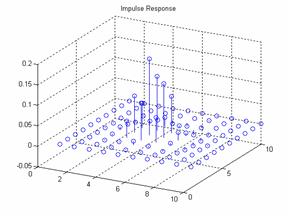
The output:

Blackman-Harris Window:
For a frequency space of 10
and a blackman-harris window of 10 the results are:
Plot of the frequency
response and the impulse response:
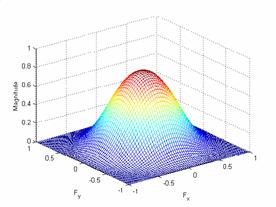

The output:

For a frequency space of 10
and a
Plot of the frequency
response and the impulse response:
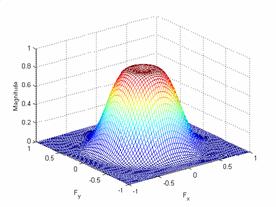
The output:

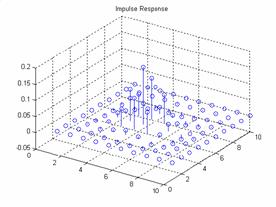
Gaussian Window:
For a frequency space of 10
and a gaussian window of 10 the results are:
Plot of the frequency
response and the impulse response:

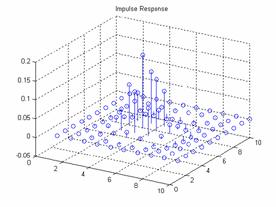
The output:

Problem Two: Beamforming
techniques
(20 points)
Describe as illustrative as possible the
difference between time-domain beamforming and frequency-domain beamforming
SOLUTION:
We will explain one
application to sonar where Beamforming is used
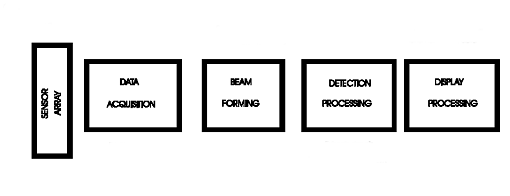
The
sensor array is composed by the antenna array that detects the signal. Then the
signals of the arrays go to the data acquisition that is in charge of
digitizing the data. Then the beam forming block generate defined beams from onmielement data (this will be explained better later). The
detection processing extract the signal eliminating the noise and the averberation.. Display processing
is how the data will be used.
The
application is sonar oriented but theory is the same to other applications.
Here there is an array of hydrophones receiving signals from an acoustic signal
in the far field. The problem here is that the phones across the array receive signals
with different time
delays, so the phone outputs are not coherent and the summer output drops.
TIME DOMAIN SONAR BEAMFORMING:
In
the next figure is shown how the displacement of the source affects the output
signal of the array. At the first figure the source is perpendicular to the
array plane and for this reason the delay of all the phone is zero, it maximize
the output of the whole array. At the second figure the source is moved from
the perpendicular and now we can see there are different phase for each signal
of the phones. We need to correct this, to do that we could implement a time
delay units on each one of the phones, with this units the incoming signal
could be adjusted to have a maximum value, simulating the perpendicular
conditions.
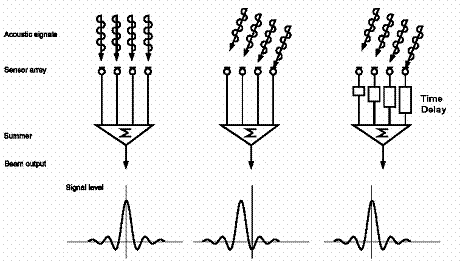
Conceptually
it works but in Sonar applications the delay of the sonar signals is too high
and it makes that orientation of the array to the signal is a difficult
problem. In order to solve this other strategies must be taken in account. One
if manage the delay fo the
signals with accelerometer measurement that compensate the time delay. Other
strategy is applying oversampling to the data and/or
using FIR interpolators.
FREQUENCY DOMAIN SONAR BEAMFORMING:
The
main aim of using frequency domain techniques for Sonar Beamforming is to
reduce the amount of hardware needed. The time domain Beamforming its efficient with small number of channels array, up to 128
phones and becomes unwieldy for large arrays.
There
are several classes of frequency domain Beamforming:
- “Conventional”
Beamforming where the array element data is essentially time delayed and
added to form beams, equivalent to spatial FIR filter.
- adaptive beamforming, where
more complicated matrix arithmetic is used to suppress interfering signals
and to obtain better estimates of wanted targets.
- high resolution beamforming,
where in a very general sense target signal-to-noise is traded to obtain
better array spatial resolution.
![]() NARROW BAND BEAM
FORMING:
NARROW BAND BEAM
FORMING:
If
the beamformer is required to operate at a single
frequency, then the time delay steering system outlined above can be replaced
by a phase delay approach. Time delay
Beamforming could be written as:
![]()
Where:
N: number of hydrophones.
Wk: is the array shading function.
fk(t):
is the time domain kth data element.
τk,r:
is the time delay applied to the kth
element data for the rth beam.
![]()
![]()
for the kth sensor
in the array:
![]()
![]()
![]()
Here we must apply an adjustment
in the phase of the beamformer in the frequency
domain in order to adjust the output of the sensor to the maximum.
CONCLUSION:
The main difference between Time domain Beamforming is that in time domain beam
forming qe apply a delay in time of the signal and in
the Frequency domain Beamforming we apply a product by exp(-jkφ)
to compensate the phase difference between the signal of each sensor.
Problem Three: Short-time Fourier transform
(20 points)
Use the cyclic convolution to provide a
mathematical formulation of a cyclic version of the filter method of the
short-time Fourier transform.
Solution:
Let the sequences ![]() be defined as follows:
be defined as follows:
![]()
![]()
Let ![]() define the following padding operator:
define the following padding operator:
![]()
![]()
![]()
![]()
Where:
![]()
![]()
So let ![]()
![]()
![]()
Let ![]()
![]()
It’s the Circular Convolution
Operation, and using the commutative property of the Circular Convolution we
obtain the following:
![]()
![]() ; where
; where![]() , denotes the circular convolution.
, denotes the circular convolution.
Problem Four: Discrete
Fourier Transform
(25 points)
Provide a mathematical description (through
demonstration) of four properties of the two-dimensional discrete Fourier
transform.
SOLUTION:
TRANSLATION
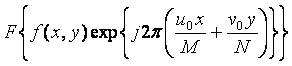
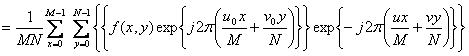
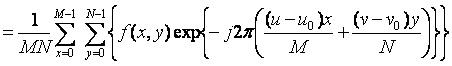
![]()
SEPARABILITY:
![]()
![]()
![]()
Where:
![]()
and
![]()
PERIODICITY:
![]()
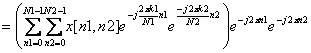
![]()
![]()
LINEARITY:
Given
g and h
![]()
![]()
![]()
![]()
![]()
CIRCULAR TIME SHIFTING:
![]()
![]()
![]()
![]()
![]()
Problem Two:
(25 points) An ideal low-pass continuous two-dimensional filter has
the value of “one” in its pass-band and the value of “zero” after its cut-off
frequencies ![]() and
and ![]() . Use the time-domain convolution theorem to obtain the
output signal, in object domain, of the filter if the input signal is
given by the equation below.
. Use the time-domain convolution theorem to obtain the
output signal, in object domain, of the filter if the input signal is
given by the equation below.
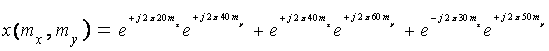
Use
the following Fourier transform identity:
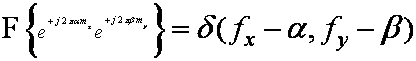
SOLUTION:
![]()
![]()
Using the time domain
convolution theorem. A convolution in time equals to the inverse
Fourier transform of the product of the Fourier Transforms of the input
and the impulse response of the filter.
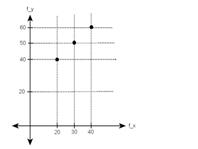
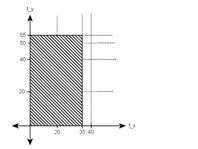
Input Signal Low Pass Filter response
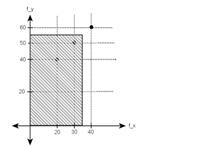
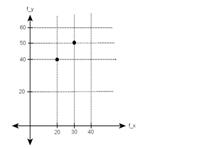
Product of Input and
Filter. Output of the System
Then the output of the Filter to the input x(mx,my) is:
![]()
Problem Three:
A. (20 points) Write in matrix form the computation of the DFT of the following signal array:

SOLUTION:
On this point we make a variation of the solution,
we use the kronecker product and circulant
matrix to compute the circular convolution just as a way to try another way to
the same result.
The Fourier Matrix for Z2:
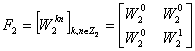
![]()
![]()
![]()
Using Kronecker products:
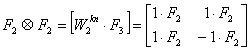
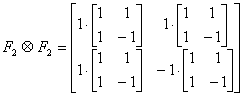

One-dimensional array scattering operator: ![]() (anti-lexicographic)
(anti-lexicographic)
Applied to the signal array:
![]()
![]()
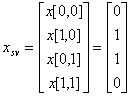
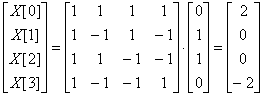
Two-dimensional array gathering operator:![]()
![]()
![]()
![]()
So ![]()
DTF: ![]()
B. (20 points) Compute the cyclic convolution, using any desired method, of the following two arrays given below. Remember that the cyclic convolution is a commutative, linear operation.
 ,
, 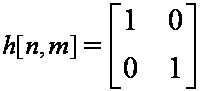
Solution:
Computing the circular matrix (BCCB):
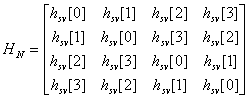
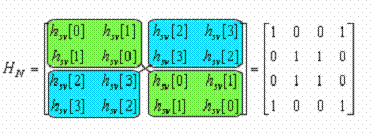
One-dimensional array scattering operator: ![]() (anti-lexicographic)
(anti-lexicographic)
Applied to the signal array:
![]()
![]()
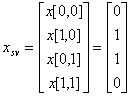

Two-dimensional array gathering operator:![]()
![]()
![]()
![]()
Cyclic
convolution: ![]()
THE SOLUTION PRESENTED BEFORE IS:
PART A:
Solution:
![]() ;
; ![]()
Where: ![]() ;
; ![]() and
and ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
DTF:
![]()
PART B
Solution:
![]()
![]()
Where: ![]() ;
; ![]() and
and ![]()
![]()
![]()
![]()
Where: ![]()
![]()
![]()
![]()
![]()
![]()
Cyclic convolution: ![]()