3. SPECGRAM and SPECGRAMDEMO

The specgram and specgramdemo function in Matlab makes a Time-dependent frequency analysis.

The specgramdemo function is a user friendly interface to make easier and significant the data provided by the specgram function. First we concentrate the efforts in the understanding of the specgram function and then we will see how the specgramdemo improves the results of the specgram function.

The specgram function do the STFT of a signal of finite time acquired at a specific sampling rate.

The parameters for the specgram function are described below:

INPUT PARAMETERS:

Any application of the specgram requires a vector, other values could be specified, if not are specified Matlab will take the default value.

specgram(a,nfft,fs,window,numoverlap)

a : Correspond to the vector of the input signal.

nfft : Specify the size of the FFT that specgram uses.

default: nfft = min(256,length(a)).

fs : Is the sampling frequency of the vector a.

default: fs=2.

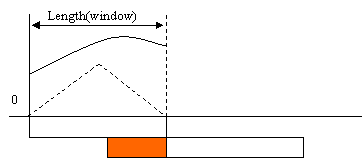
window : This is the kind of windowing function that will be in the nfft space in

the a vector.

You must care that: length(window)<nfft.

default: periodic Hann (Hanning) window of length nfft.

You can use one of the following windows provided for matlab:

numoverlap : It defines how much the new window overlap the one before.

default: numoverlap = length(window)/2.

You must care that numoverlap< length(window).

Graphically each of the values mentioned above are:

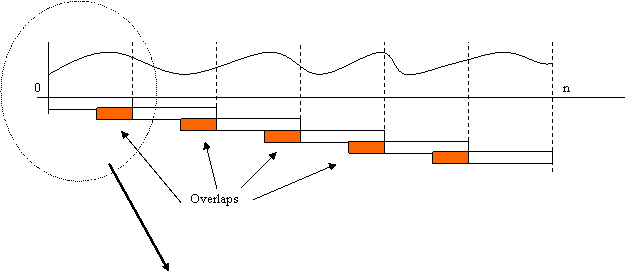
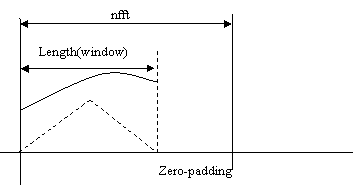
Following to this, each segment of the vector a, is zero padded and the FFT is calculated:

OUTPUT VALUES:

The FFT of each segment is stored in one column vector that is join to make the matrix B that correspond to the output of the specgram function.

Another outputs provided by the specgram function are the column vectors t and f.

The vector t contains the time at each of the windows starts. A way to calculate the number of rows of this vector is (is the same number of columns of B):

where n is the length of the vector a.

Observation: Note that the k number doesn’t depends of the nfft number this is because the nfft affects the frequency resolution of the window that I’m observing. Be aware that the length(window)≤nfft. This is because a the fft returns a vector (of length nfft) equal to the sum of length(window) and the zeropadding that we must do.

The vector f contains the frequencies at which the FFT is calculated. The length of this vector is the nfft specified in the input parameters.

Observation: This vector depends of the nfft value. If you increase the nfft value the vector f will be longer. The ratio between nfft and the length(f) is the double.

f1

f3

f2

f

v

e

c

B

t

M

A

T

R

I

X

o

r

fnfft

t1

t2

t3

tk

t

v

e

c

t

o

r

Each column of the vector B contains the FFT of each product window-signal.

Here there are some examples of syntax:

specgram(a) This makes the specgram of a with default values.

nfft=min(256,length(a)).

fs=2.

window=hann(nfft).

numoverlap= length(window)/2.

B = specgram(a) This assigns the ouput of the specgram to the matrix B.

nfft=min(256,length(a)).

B = specgram(a,nfft) This makes a specgram at specified value nfft.
If nfft=256 then is equal to the one before.

[B,f] = specgram(a,nfft,fs) Here the frequency output vector is returned.

And the Sampling frequency is specified.

[B,f,t] = specgram(a,nfft,fs) Here the time vector is returned.

B = specgram(a,nfft,fs,window) Here a window is specified.

B = specgram(a,nfft,fs,window,numoverlap) Here an overlap is specified.

Example:

With the next signal as vector a (#samples=2000 , fs=1000):

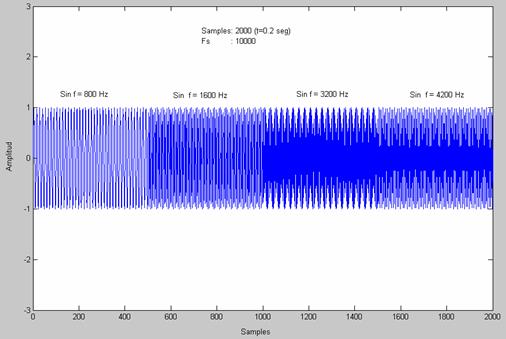
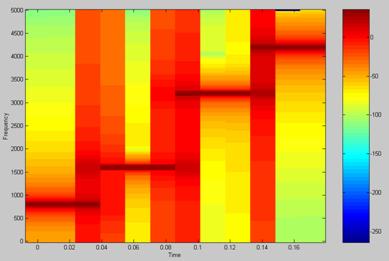
Then with the next command:

>> specgram(output,256,10000,hann(256),100),colormap(jet),colorbar;

The output is:

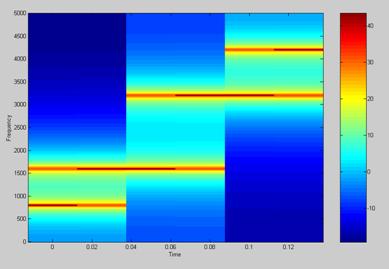
Another example with the same signal:

>> specgram(output,1000,10000,hann(750),500),colormap(jet),colorbar;

The output is:

As we can see the second graph has less k for this reason appear fewer segments over the time axis. In the second graph the horizontal lines looks thinner it means higher spectral resolution; this is because the nfft value of the second graph is 1000 instead of 256.

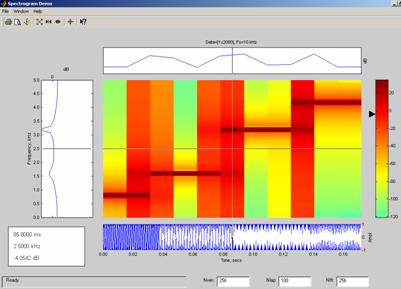
The specgramdemo is basically a user friendly version of the specgram function. On this function you have to specify two things the time sequence and the fs (sampling frequency).

You must write on the command line of Matlab the following:

>>specgramdemo(a,fs);

The tool will work with default values. Here there are the two graphs of the examples given before.