Computer Homework 3

In this computer homework you will design FIR filters using matlab. FIR filters are described by linear constant coefficient equations of the form

y[n] = b₀x[n] + b₁x[n-1] + b₂x[n-2] + ... + b_qx[n-q],

and the transfer function will be of the form

H(z) = b₀ + b₁z^-1 + b₂z^-2 + ... + b_qz^-q.

IIR filters have equations of the form

y[n] = - a₁y[n-1] - a₂y[n-2] - ... a_py[n-p] + b₀x[n] + b₁x[n-1] + b₂x[n-2] + ... + b_qx[n-q],

and transfer functions of the form

H(z) = b₀ + b₁z^-1 + b₂z^-2 + ... + b_qz^-q / a₀ + a₁z^-1 + a₂z^-2 + ... + a_qz^-p .

FIR filters have a finite impulse response because there is no feedback. When the input stops, the output stops after at most q steps. IIR filters have feedback, and the output can continue even though the input is zero.

After designing the filters, you will filter the given signal and listen to it.

Designing FIR filters in Matlab

Matlab has many commands for designing FIR filters. We will use the impulse truncation method for the design. To design a LP FIR filter use:

>>b=fir1(N,Wc);

N is the order of the filter, and Wc is a normalized cutoff frequency. It is the frequency in radians/sample divided by pi. For example, if we want a cutoff frequency of 0.2pi rad/sam, use 0.2 in matlab. Designing FIR filters with this method is iterative, so we may have to find the coefficients b many times. Change N and Wc as necessary to get the lowest order filter that meets the specifications.

************************************************

Ex.

Design an FIR LPF of order 10 with a cutoff frequency of 0.2pi rad/sam. Read the file input.wav, filter the signal using the designed filter, and play it over the speaker.

clear;

[x,fs]=wavread('c:\input.wav');

b=fir1(10,0.2);

y=filter(b,1,x);

sound(y,fs);

************************************************

Computer Homework 3:

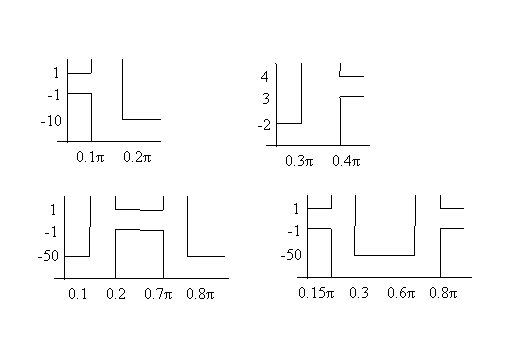
Design four linear phase minimum order FIR filters for the specifications given below. Plot graphs of magnitude and phase that show that they meet the specifications.

1.