Prepared by: Dr. Shawn D. Hunt

Contributions by:

Iñaki Olivares

Ricardo Figueroa

Angel Torres

This document outlines part the research being done in lossless compression by my students and I.

I. Lossless Image compression

We want lossless image compression, or compression where we can recover the original image exactly. There are two main reasons for this. First is that all the uses of the images are not known at present. It may be desirable at some future date to use the images for studies not planned for at present. If some of the image is lost during compression it may render them unsuitable for future purposes. Also, some of the applications use automatic pattern recognition schemes. In many of these schemes it is not known exactly what information is used to perform the pattern recognition. For example, in using neural networks to detect some element in the picture, it is the net that organizes itself to use features in the image for detection. Because these features are chosen by the net, and the parallel interaction of the features when detection takes place may not be known to the user, it is difficult to predict the performance of the system if some of the image is lost. Thus, it may be that some systems would work with a certain compression scheme, but new algorithms may not.

Most compression schemes used now are lossy, and so cannot be used. At the present time, most algorithms for lossless compression use linear predictive coding. The approach to be studied here will be to investigate the advantages of using non-linear predictive coding. A theoretical background for lossless compression, various contemporary compression algorithms, and our present research are presented below.

A. Theoretical Background

Working with computers, the data is represented, or coded, with binary numbers. Let each data be a member of the set of numbers{a₁, a₂, . . . a_N}. For example, if we are coding numbers from 0 to 255, then N=256, and a₁=0, a₂=1, . . . , a_N=255.

One popular method of coding data using bits is Pulse Code Modulation, or PCM. This is the format used in most A/D, D/A and dsp chips. In PCM, all letters in the alphabet are coded with an equal number of bits, so in the example above where N=256, the length of the code is 8 bits (table 1).

If we have a sequence of data coded in PCM, lossless compression is accomplished by coding the data, or transforming and then coding the data, in a new way using fewer bits to represent the data. The fundamental question in lossless compression is: Given a sequence of data to be coded, what is the minimum number of bits that can be used to code the sequence. This turns out to be very difficult to determine in most real cases, but we may be able to determine good approximations. To try and do this, we can use the notion of information and probabilistic modeling.

Assume that a source outputs data from the allowed set according to a certain density function. Every time the souce outputs a number, information is transmitted. Information can be viewed as a measure of uncertainty, and is based on how likely or unlikely each value in the allowed range is. Numbers that have a high probablility of being output conveigh less information than numbers that have a low probability. In the extreme case where the probability of a number is one, then we know what the next data is before it is output, and it gives us no information. This idea leads to the following definition of information for each number in the allowed set:

I_i = log= - log p(a_i).

As can be seen, the information is inversely proportional to the probability. The log was proposed by Hartley [5.6], and gives the entropy, defined below, desirable characteristics.

If we use a base 2 log, then the units for information is bits.

The average information output from the source can be measured in bits per data, and is called the entropy. Lugwig Botlzmann is generally attributed with a formula for entropy, R. Hartley used the concept of entropy applied to information capacity, and Shannon further expanded the idea of entropy in communication with the information content of a message [4]. The first order entropy is the expected value of the information,

H(a)= -p(a_i) log₂( p(a_i) ).

This can be used as an estimate of the average number of bits needed to code each data, if each data is coded independently from the others. This does not tell us how to code the data, or even if there is a code that uses this many bits per data, but it does give an approximation to the lower bound for the average number of bits per data. This can be very valuable in looking for good codes. If we are coding the data independently and the number of bits per data used is close to the first order entropy, then we know we have a good code, and do not have to keep looking for others.

The joint entropy of two data values can be defined as,

H(a₁,a₂)= -p(a_i,a₂) log₂( p(a_i,a₂) ),

and higher order entropies can be similarly defined from the joint density functions,

H(a₁, . . . ,a_M) = -. . .p(a_i, . . . ,a_k) log₂( p(a_i, . . . ,a_k) ).

These higher order entropies can be used as estimates of the number of bits needed to code the M data values together. It is not difficult to show that (see [5,5.5])

with equality if and only if they are independent. This means that in general, we can code with fewer bits if we code more than one data at a time. The drawback to this is the complexity of the code. Suppose we want to code numbers from 0 to 255. If we code each data independently, then we will need 256 codes, one code for each value allowed. If we code two numbers at a time, then there are 256² possible combinations, so we need 256² = 65,536 codes.

If the data are not independent, then knowing the data that came previously should give us information, or lower the uncertainty of the next data. If we take this into account when coding, we should be able to use fewer bits. How many fewer bits? We can get an approximation for this using conditional entropies. The conditional entropy is the average information in a data, given that a set of other data is known. In a causal system, the set of data is usually the previous data output from the source.To calculate the entropy of a given that a set of data s is know, we use

H(a|s=s_k) = -p(a_i|s_k) log₂( p(a_i|s_k) ).

If we average over all possible sets of data, we get the conditional entropy

H(a|s) = p(s_k) H(a|s=s_k),

= -p(a_i,s_k) log₂( p(a_i|s_k) ).

For example, let a₁ and a₂ be consecutive data from the sourse, and suppose we want to know how much information is contained in a₁ given that a₂ is known. We can then use

H(a₁|a₂) = -p(a_i,a_j) log₂( p(a_i|a_j) ).

Again, it can be shown [5] that

or in general,

with equality if and only if a and s are independent. This says that if a and s are not independent, then knowing s reduces the uncertainty or entropy of a. So if we code a taking s into account, we can use fewer bits.

In the example above using two consecutive data from the source, if the data are independent, then knowing the previous data will not lower the uncertainty of the next data. If the data are not independent, then the previous data should lower the uncertainty, or lower the entropy of the data. Thus, the entropy is lower in the dependent case, since knowledge of previous data reduces the uncertainty of the next data from the source. Coding the data taking into account the statistical relationship of the data will lower the average number of bits per data needed, but these context sensitive codes are more complex. They are called context sensitive, because the code for the next data will depend on the previous data. For example, assume we are coding a message in the English language. Suppose we have received a 't' then an 'h'. The code for the next letter does not have to include all the letters from a to z, and would only include the possible letters that follow 'th'. If we receive an 'i', the code for the following letter will be a code for all the possible letters that follow 'thi'. This means the code is very complex and computationally intensive, making both coding and decoding slow.

It was shown above that if the data are not independent, then the joint and conditional entropies are smaller than the first order entropy, so coding more than one data at a time, or coding using context sensitive codes will give a lower average bit rate. The drawback is that the codes are more complex. Two things could be done to alleviate this. The data could be coded assuming independence, resulting in a higher average bit rate. Or, the data could be transformed into an independent sequence, and then coded. This second method is the most popular lossless compression technique.

Compression is then divided into two steps, the decorrelation stage, where we try to produce an independent sequence, and the coding stage. One theoretical justification for this method can be found in Wolds Decomposition Theorem [1,2,3].

The theorem states the following [3]:

Let x[n] be a wide sense stationary (WSS) process. Then x[n] can be written as a sum of two processes,

where x_r[n] is a regular process, and x_p[n] is a predictable process, and x_r[n] is orthogonal to x_p[n].

Regular

In general, a process is regular if it is not band limited. We use the term regular to mean also that its power spectral density has no impulses. Let S_r(e^j) be the spectral density of x_r[n]. Thus, S_r(e^j) is the Discrete Time Fourier Transform of the autocorrelation of x_r[n]. Or,

S_r(e^j) =R_r[m] e^-jm.

Since this process is regular, its power spectral density is a continuous function of , and can be decomposed as

If x_r[n] is real, then this simplifies to S_r(z) = ² Q_r(z) Q_r(z^-1). The elements of a real regular process are independent.

Predictable

A process x_p[n] is predictable, if

x_p[n] = h_k x_p[n-k],

where h_k are constants. This means x_p[n] can be determined exactly from a linear combination of its previous values.

If we assume that the data we are trying to compress is a WSS process ( and this is usually not the best assumption), then we can decompose it as suggested by Wolds decomposition. Then,

We first find a prediction model for x_p[n], then subtract this prediction from x[n], so that x_r[n] remains. Since x_r[n] is a regular process, there exists a linear filter, called the whitening filter, that converts x_r[n] into a white-noise (indepentent) process, say x_w[n]

We then code and save the prediction model (the h_k coefficients) , and x_w[n]. The idea is to save only x_w[n], and the prediction model of x_p[n] instead of the original signal. This leads to a reduction of data in many cases, because x[n] has a larger first order entropy than x_w[n]. It will thus take fewer bits to independently code each sample of x_w[n] than the original signal x[n].

From the discussion above, it seems that we will have to find one linear filter to remove the predictable part, then another linear filter to whiten the regular process that remains. It turns out that this is unnecessary, because one filter is the predictor of the three processes x[n], x_r[n], and x_p[n] [5].

Let H(z) be the (one step) predictor of x_p[n],

x_p[n] = h_k x_p[n-k],

and

H(z) = h_k z^-k.

Using this filter as shown in figure 1, produces the white noise output in one step.

After prediction, the remaining part of the signal is white-noise, x_w[n]. This white noise signal is often called the prediction error, as it is the difference between the original signal, and the output of the linear filter H(z). How do we best code this? We can use entropy coding. Entropy coding works on the principle that some of the numbers in the allowed range are used more often than others. Instead of giving the same length code to each number, the ones that are used more often (more probable, and have less information) are given a shorter code than the ones that are used less often (less probable, and have more information). Huffman and Arithmetic coding are the two most popular types of codes used in lossless compression. An example using a Huffman code is given below.

Example:

Suppose we have a white random process x[n], where x[n] can take four values, -5, -2, 2, and 5. Since x[n] can take on four values, we could use two bits to code x[n]. For example, we could let -5 be 00, -2 be 01, 2 be 10, and 5 be 11.Each value of x[n] would then be coded with 2 bits, and the average length of each code is two. Notice that each code has the same length. This is the best we can do if x[n] takes on all four values with the same probability. If the probability for each values is different, then we can use different lengh codes and do better. Let x[n] have the following probability density,

p(-5) = 0.2

p(-2) = 0.1

p(2) = 0.6

p(5) = 0.1.

If we code -5 as 10, -2 as 110, 2 as 0, and 5 as 111, then the average code length is:

2 (0.2) + 3(0.1) + 1(0.6) + 3(0.1) = 1.6 bits. For this simple example the savings is not spectacular, but the average code length goes from 2 bits to 1.6 bits for each value.

Lets take a look at how these ideas are used in actual practice, and how some of the assumptions are violated. The first step, as mentioned above, is to find a linear filter with a white noise output. This step is typically called predictive coding. The signal to be compressed is typically modeled as an ideal signal coming from a linear FIR filter and additive noise. (Figure 2)

This is the first simplification of the problem. Above it was shown that in general, a WSS process has a predictor that is of infinite length. The finite length predictor is only optimal if the sequence is Markov. Since an infinite length filter cannot be implemented, a linear FIR filter is usually used [6]. This method is computationally attractive, but is usually not optimal and the resulting error in the prediction is not white. Non-linear finite filters, or predictors, can be better, but tend to be computationally expensive.

The second violation of assumptions is in the signals to be predicted. The signals are typically not WSS. If we look at an image, for example, it changes from one part of the image to another. It is not completely random, however, and the image may be modeled as stationary in small regions. This 'small region' stationarity is addressed in two ways in practice. One way is to divide the image into small parts, and find a different prediction filter for each part. The other way is to use an adaptive filter. This filter will then adjust to the image, and change as the image changes.

B. Contemporary Research

1. Linear Prediction Techniques

a. Prediction tree

In [7], Memon et al. constructed a prediction model by stating the differential coding method as a graph problem. First, the digital image P is represented as a difference graph D, replacing every pixel in P with a vertex. Then, the vertices are connected vertically and horizontally to its four adjacent neighbors(4-neighborhood model), and each connection is weighted with the difference of the corresponding two pixel values. A 4 x 4 digital image and its difference graph are shown in Fig. 1 (a)-(b) [7].

Given the value of any pixel in a digital image, the remaining pixels can be predicted using a spanning tree of its difference graph, which Memon et al. called a prediction tree of image P. Fig. 2 [7] shows a prediction tree of the image in Fig 1(a).

Notice that for each image P, there is a large set of prediction trees, so the problem now is finding the prediction tree in which the entropy of the weights is minimized. Memon showed that the minimum entropy prediction tree has the smaller sum of the absolute weights of prediction errors. This tree is called a minimum absolute weight prediction tree or MAW tree. The MAW tree can be computed in time linear with size of the image [7].

Two methods were applied to decorrelate multispectral images:

(a) Backward adaptive.

The first method proposed was to use the optimal prediction tree of the image in the current band on the image in the next band, instead of using an optimal prediction tree for each image. Since the optimal prediction trees for adjacent spectral bands are similar("have more than half their edges in common" [7]), this can be done without important loss in performance. The steps for transmitting and coding the sequence of images is the following:

1. The first image is compressed and transmitted using any known method.
2. Decorrelate the current band using the MAW tree of the previous band.

(b) Forward adaptive

The second method proposed was to compute a single optimal prediction tree for a set of bands and use it to decorrelate each image of the set. This prediction tree is the MAW tree of the image set cumulative difference graph. The weights on the edges of this graph will be the sum of the weights corresponding to that edge on each image of the set. There is an additional cost in this method, since the shape of the MAW tree and the weights on the edges have to be transmitted. However, this cost is distributed over the images in the set.

b. Linear vector prediction

In [8], a linear prediction model is used to estimate the pixel vectors along each scanning line of the image. A pixel vector is composed of all the pixels corresponding to the same raster position across different spectral bands, Y_n = (Y_n(1), Y_n(2), ..., Y_n(k))^t, where k is the number of spectral bands and n is the position within a given scanning line of the image frames. Along each scanning line, the coming pixel vector can be estimated by a linear prediction of the two previous pixel vectors.

Y_n^' = AY_n-1 + BY_n-2 (1)

The coefficient matrices A and B are determined using the least-mean squared criterion, using the following set of equations,

A = R₁^tR₀^-1 - (R₂^t - R₁^tR₀^-1R₁^t)(R₀ - R₁R₀^-1R₁^t)^-1 R₁R₀^-1 (2)

B = (R₂^t - R₁^tR₀^-1R₁^t)(R₀ - R₁R₀^-1R₁^t)^-1 (3)

R₀ = E[ Y_nY_n^t ] (4)

R₁ = E[ Y_nY_n-1^t ] (5)

R₂ = E[ Y_nY_n-2^t ] (6)

where E[] is the mathematical expectation and R₀, R₁, R₂ are the autocorrelation, the lag-one and lag-two cross-correlation matrices, respectively.

After estimating the pixel vector, the residual vector, given by,

e_n = Y_n - Y_n^' (7)

is entropy encoded using the shift Huffman encoder. It is assumed that the probabilities of the error values in each spectral band follow a Laplacian distribution.

The prediction is carried out to the difference between the raw pixel vector and the mean vector. The compression algorithm described by Xu et al. in [8] is as follows,

1. Scan the image data files. Calculate the three correlation matrices, R₀, R₁, R₂ and the mean vector of the raw data. The mathematical expectation is replaced by the sample averaging.
2. Calculate the prediction coefficient matrices A and B.
3. Subtract the mean vector from each raw data vector in the image files.
4. For every raster line of the data
   • From the third vector calculate the residual vector using Eq. (1) and (7). The first two residual vectors in each raster line are just the mean-subtracted vectors.
   • Send k elements to k frequency counters alternatively to calculate the frequency of occurring of the error values for each band of error images. Initialize k Huffman encoding processors.
5. Subtract the mean vector from each raw data vector in the image files again.
6. For every raster line of the data
   • From the third vector calculate the residual vector using Eq. (1) and (7). The first two residual vectors in each raster line are just the mean-subtracted vectors.
   • Send the k elements to k Huffman coding processors alternatively and record the codes as the outputs.
   • Record the line index indicating the number of bytes in the code for this line.

c. Adaptive 2-D and 3-D prediction of pixels

In [9], multispectral images are decorrelated using 2-D and 3-D adaptive linear prediction models. A pixel X on a given band Z can be predicted with information from surrounding pixels(E, F, G) in the same band and pixels(A, B, C, D) in the previous band Z-1(Fig. 3 [9]). In Fig 3, the four pixels in each band correspond to the same location in ground.

The 2-D adaptive predictor uses information of the local gradients of pixels in the same band as shown in the following equation,

X^' = (G) + (F). (8)

The constants and weight the importance of the pixels(E, F) used in the prediction.

The 3-D adaptive predictor is a function of pixels in the local and the previous band. The prediction of pixel X is given by,

X^' = D + () + () (9)

where and are function of pixels in both bands, and and are functions of the local gradients in the previous band. The correlation of the residuals in the 2-D predictor is higher than the 3-D predictor in bands 1-8, while it is similar in bands 9-16. For this reason, a combined 2-D/3-D predictor can be constructed to increase the performance in bands 1-8 and decrease the complexity in bands 9-16.

The residuals are quantized based on the local statistics(mean and variance) of the 2-by-2 blocks in which the residual image is divided. Fig 4 shows the local adaptive quantizer structure [9].

If the quantization error exceeds a predefined maximum threshold, a lossless quantizer is chosen. The quantized image is encoded using a variable length Huffman code while the quantizer overhead is encoded using a Huffman and Run-Length code.

2 Transformation Techniques

a. Karhunen-Loeve Transform(KLT) / Discrete Cosine Transform(DCT)

The following algorithm, described in [10], decorrelates the set of images spectrally using KLT. Then, the set of eigen images produced are spatially decorrelated using DCT. Fig 5 [10] shows the block diagram of the encoder.

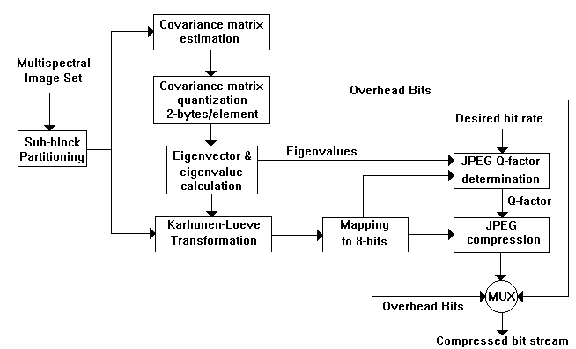
The set of multispectral images are first divided in sub-blocks of N non-overlapping images. Afterward, each sub-block is processed by the KLT module represented with four blocks in diagram(Fig. 5 [10]). This module consist of the following steps:

1. Calculating the cross-variance matrix of the sub-block set.
2. Quantization of the covariance matrix floating point values to 2 bytes per element.
3. Calculate the N order eigenvectors of the covariance matrix.
4. Form an N-by-N KLT transformation matrix with the eigenvectors.
5. Build the set of eigen images by matrix multiplication of the KLT transformation and the vectors formed of the pixels values in the same raster position.

Since the set of eigen images are in floating point format, the next module quantize them before they are coded by the JPEG algorithm in the last module. For the first two high-dynamic range eigen images, a nonlinear 8-bit quantizer was used based on the uneven histogram of the data. Finer quantizer steps were allocated in the large central portion of high dynamic range. The nonlinear quantizer is given by,

Y = 255 / (MAX^exp)X^exp (10)

where: X is the eigen plane value (floating point), Y is the eigen image value (an integer from 0-255), exp is the nonlinearity index (0-1 range), and MAX is the maximum value of the eigen plane. A linear 8-bit quantizer was used to quantize the remaining low-dynamic range eigen images.

The last module is the JPEG compression of the eigen images. The quantization scale table for the DCT coefficient (Q table) has been modified to match the spatial characteristics of the eigen images. Since it is desirable to maintain the spectral fidelity of the data, the lower and higher eigen images were coded with the same level of accuracy irrespective of the variances or the overall mean square error[10]. Therefore, the bit assignment was chosen so that all the reconstructed eigen planes had a uniform overall coding error. The approach was a compromise between performance and implementation complexity. Four methods were proposed, and they were derived from extensive experimentation. In the optimum method, an arbitrary mean square error(MSE) is selected for the first eigen image and the effective MSE for the remaining eigen images is calculated as,

MSE(n) = L(1) x B(n) / B(1) (11)

where n = {2,3,...}, L(n) = MSE for the n eigen image, and B(n) is the binary width to quantize eigen image n. The lowest quality factor (Q) is selected for each eigen image so that the effective MSE is less than or equal to the MSE calculated with equation (11). It is necessary to construct a look-up table of MSE vs. Q for each eigen image. The second method is similar to the one described above, but some of the low-variance eigen images are replaced by their mean value. The third method uses the same Q factor for all the eigen images. In the fourth and last method, the Q factor is varied according to the variance and the initial quantization error of each eigen image.

b. Adaptive transform coding-spatial

This method transforms the multispectral images spatially using the DCT transform and then normalizes, quantizes and codes the transform coefficient using a bit allocation map based on an activity parameter[11]. First, the image data is partitioned into small blocks of 16-x-16. Each block is transformed spatially using DCT transform. The transformed blocks are classified into one of several classes based on a block activity parameter (e.g. the ac energy of each block). A bit allocation map is formed based on the activity of each transform coefficient within a class so that more bits are assigned to areas of high activity and less bits to areas of low activity. Using this information, the transform coefficients are normalized, quantized and coded.

3. Vector Quantization Techniques

a. Vector Quantization

In this first vector quantization technique [11], the multispectral images are compressed spatially using the conventional vector quantization algorithm. First, the image is divided into many small blocks (4-x-4), which are represented as vectors. Each input data vector is compared with a list of vectors of the same dimension as the input data vectors(codewords). The whole list of codewords is known as codebook. The codeword with the smallest distortion is chosen to represent that input vector. The indices of the codewords that represent each vector are transmitted through the channel. At the receiving end, the decoder reconstructs the image by looking for the codeword in the codebook using the corresponding index. For this particular implementation, a codebook is generated for each image frame, which is transmitted with the coded data. In order to reduce the encoding complexity of training the codebook and searching for the codeword, the codebook is arranged in a two level tree in which we have n1 codewords in the first level and n2 codewords for each codeword in the first level. This reduces the overall computation from (mF + 1)2ⁿ op/pixel to m(2ⁿ¹ + 2ⁿ²) op/pixel, where m is the iterations in codebook training, n is the length of the codebook, and F is a fraction of the image used for the training.

b. Feature Predictive Vector Quantization(FPVQ)

This technique is a combination of vector quantization and linear prediction techniques [12]. For simplicity, the method will be explained first using only two bands. Afterward, the necessary steps for its expansion to multiple bands will discussed. Each band is partitioned into non-overlapping m x m blocks. Vectors X₁ and X₂ represent the pixels within the block for band 1 and band 2, respectively. First, X₁ is vector quantized. Then, X₂ is predicted from the value of the quantized vector X_vq1. We denote the predicted value of the band 2 vector X₂ by X_p2. The prediction error e = X₂ - X_p2 is vector quantized if ||e||² exceeds some predefined threshold. Otherwise, the residual vector is ignored and the reconstructed vector is simply the predicted vector.

Different from method III-A, the codebook is not transmitted. A unique codebook was trained using the Lloyd algorithm and used for all input images. The only data transmitted are the indices from the vector quantizations of vectors X₁ and residual error, e, and a bit used to indicate the decoder that ||e||² is greater than the threshold value.

Two types of predictors were used : the affine predictor and a nonlinear predictor. The affine predictor is given by.

X_p2 = A^*X_vq1 + B^* (12)

where A^* is a matrix of size k x k and B^* is a column vector of dimension k. The solution to the affine predictor is,

A = E[(X₂ - E[X₂]) (X₁ - E[X₁])^T]C^-1_X1 (13)

where

C^-1_x1 = E[(X₁ - E[X₁]) (X₁ - E[X₁])^T] (14)

and

B = E[X₂] - A[E[X₁]]. (15)

E[] is the expectation over the 2k-dimensional joint probability distribution function of vectors X₁ and X₂.

To design the nonlinear predictor, we notice that the domain of the predictor f() is finite and consists of the codeword vectors, c_1i, in the size N codebook. The optimal predictor, that minimizes D = [||X₂ - X₂^*||² | X_vq1] over all estimates X₂^*, is generated by finding f(c_1i) for each i{1,2,...,N} that minimizes the conditional distortion,

D_i = E[||X₂ - f(c_1i)||² | Q₁(X₁) = c_1i] (16)

where Q₁(X₁) is the quantized value of vector X₁. The solution to this problem is given by,

f(c_1i) = E[X₂ | X₁ R_i] (17)

where

R_i = {X₁: Q₁(X₁) = c_1i} = {X₁: E₁(X₁) = I}. (18)

A complete specification of the optimal nonlinear predictor f() requires the tabulation of the conditional mean of X₂ given R_i for each of the N regions R_i.

The method described above can be applied to multiple bands(e.g. more than two) using one of the following two techniques:

1. Vector quantize vectors in one band and predict the vectors in the remaining bands from this vector.
2. Separate the bands in two sets M and L. Construct M parallel FPVQ modules in which vectors from set L are vector quantized and used to predict a vectors from several bands of L.

C. Results and Accomplishments

During the 1997-98 academic year, research was focused on implementing a lossless compression algorithm for level 1 AVHRR image data. More information on this data can be found in [13].

1. Theoretical

Information content experiments of the AVHRR images were done using matlab and C. These were done to determine the first order and conditional entropies to be used as benchmarks for the data reduction algorithm. Also, various nonlinear fir filters were tested as predictors. As expected, they performed better than linear predictors, but were computationally more intensive. The results warrant further investigation.

2. Applied

A program that takes level 1 AVHRR imagery and losslessly compresses and decompresses it was implemented in C. The program has been compiled and run on the PC, Apple, and UNIX environments. The program consists of a linear predictor, and Huffman coding. Typical compression rates are 2.5 to 1. This program has been developed for immediate use here at the Earth and Space studies lab for data distribution, and to be used for further development. It will be the benchmark for nonlinear techniques, and the code will serve as the framework for more advanced implementations. The program has been implemented in modules, so that easy substitution of the predictor or coder is possible. This means that the linear predictor can be substituted with nonlinear ones by simply changing a subroutine, and the huffman coder could be substituded for an arithmetic coder if desired.

The data is presently being stored on 4mm tape in the Earth and Space Studies laboratory. This is a typical method of data distribution, but has several drawbacks. It

requires the user to have a 4mm tape reader, and data access on tape is generally slow.

We would like to make it possible to distribute the data on CD-ROM. This will make it more convenient to the user, as CD-ROM drives are now ubiquitous, but we would also like the use of CD-ROMs to be cheaper and faster.

For comparison, a 4mm tape of 90m length holds 2Gb of information, and costs around $8 dollars. CD-ROMs hold 680Mb of data and cost around $3 dollars. So the 90m tapes hold 2.94 times more data than a CD-ROM, and cost 2.67 times more. We would like to achieve 2.94 to 1 compression ratios, so that one CD-ROM could hold the same amount of information as one tape. Even at the present compression ratios of 2.4 to 1, the CD-ROM has a cost of approximately 0.184 cents per Mb, compared with 0.4 cents per Mb for tape.

The AVHRR images have an average size of 90Mb each. The time to read an image file of this size from tape is approximately 4 minutes. The time to read this compressed image from CD-ROM and decompress it using this program is approximately two minutes and seven seconds running on a 266MHz PC. So using CD-ROMs is not only cheaper, but faster for the end user. The only drawback is that the images must be compressed, and put on CD-ROM at the receiving station. A 90Mb image takes about 7 minutes and 12 seconds to compress on a 266MHz PC.

REFERENCES

[1] H. Wold, The Analysis of Stationary Time Series, 2nd. Ed., Almquist and Wicksell, Uppsala, Sweden, 1954 (originally published in 1934).

[2] A. Papoulis, "Predictable processes and Wold's decomposition: A review," IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 33, no. 4, pp.933- 938, August, 1985.

[3] M. Hayes, Statistical Digital Signal Processing and Modeling, John Wiley, 1996.

[4] Dwight Mix, Random Signal Processing, Prentice Hall, New Jersey, 1995.

[5] A. Papoulis, Probability, Random Variables, and Stochastic Processes, McGraw Hill, New York, 3rd, ed., 1991.

[5.5] S. Wilson, Digital Modulation and Coding, Prentice Hall, New Jersey, 1996.

[5.6] R. Hartley, "Transmission of Information," Bell System Technical Journal, vol. 7, no. 3, pp. 535-563, July 1928.

[6] N. S. Jayant, and P. Noll, Digital Coding of Waveforms, Englewood Cliffs,

Prentice Hall, 1984.

[7] N. D. Memon, K. Sayood, and S. S. Magliveras, "Lossless Compression of Multispectral Image Data," IEEE Trans. Geosci. Remote Sensing, vol. 32, pp. 282-288, March 1994.

[8] K. Xu, K. Kajiwara, and H. Okayama, "Error-free compression of multispectral image data using linear vector prediction," in Proc. IGARSS '93, IEEE Press, 1993, pp. 1874-6.

[9] B. V Brower, D. Couwenhoven, B. Gandhi, C. Smith, "ADPCM for advanced LANDSAT downlink Applications," in Conference on Signal, Systems and Computers, A. Singh, eds., IEEE Computer Society Press, 1993, pp1338-41.

[10] J. A. Saghri, A. G. Tescher, and J. T. Reagan, "Practical transform coding of multispectral imagery," IEEE Signal Processing Magazine, vol.12, pp. 32-43, Jan. 1995.

[11] C. Y. Chang and R. Kwok, "Spatial compression of Seasat SAR imagery," IEEE Trans. Geosci. Remote Sensing, vol. 26, pp. 673-85, Sept. 1988.

[12] S. Gupta and A. Gersho, "Feature predictive vector quantization of multispectral images," IEEE Trans. Geosci. Remote Sensing, vol. 30, pp. 491-501, May 1992.