SOLUCIÓN DE
SISTEMAS DE ECUACIONES
USANDO
MATRICES Y SU TI-89
Hecho por: Elvin M. concepción
Una matriz es una tabla rectangular
de números o elementos de un anillo (véase
Álgebra). Una de las principales aplicaciones de las matrices es la representación
de sistemas de ecuaciones de primer grado con varias incógnitas. Cada fila de
la matriz representa una ecuación, siendo los valores de una fila los
coeficientes de las distintas variables de la ecuación, en determinado orden.
Una matriz se representa normalmente
entre paréntesis o corchetes:
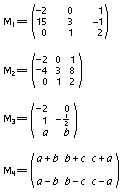
En las matrices anteriores, a, b y c son números cualesquiera. Para delimitar la matriz, en vez de
corchetes, se pueden utilizar también dos rectas paralelas a cada lado. Las
líneas horizontales, denominadas filas, se numeran de arriba a abajo; las
líneas verticales, o columnas, se numeran de izquierda a derecha. Utilizando
esta notación, el elemento de la segunda fila y tercera columna de M1
es -1. Una fila o columna genérica se denomina línea.
El tamaño de una matriz está dado por el número de
filas y el de columnas en este orden, así M1,
M2, M3 y M4
son de tamaño 3 × 3 (3 por 3), 3 × 3, 3 × 2 y 2 × 3 respectivamente. Los
elementos de una matriz general de tamaño m
× n se representan normalmente
utilizando un doble subíndice; el primer subíndice, i, indica el número de fila y el segundo, j, el número de columna. Así pues, el elemento a23 está en la segunda fila, tercera columna. La matriz
general
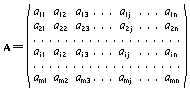
se puede representar de forma abreviada como A = (aij), en donde los posibles valores de los
índices i = 1, 2, ..., m y j
= 1, 2, ..., n se han de dar
explícitamente si no se sobrentienden. Si m
= n, la matriz es cuadrada y el
número de filas (o columnas) es el orden de la matriz. Dos matrices A = (aij) y B = (bij), son iguales si y sólo si
son de igual tamaño y si para todo i
y j, aij
= bij.
Si A = (aij) es una matriz cuadrada,
los elementos a11, a22, a33, ... forman la diagonal principal de la matriz. La
matriz traspuesta AT de
una matriz A es otra matriz en la
cual la fila i es la columna i de A,
y la columna j es la fila j de A.
Por ejemplo, tomando la matriz M3
anterior,
![]()
es la matriz traspuesta de M3.
La adición y la multiplicación de
matrices están definidas de manera que ciertos conjuntos de matrices forman
sistemas algebraicos. Consideremos los elementos de las matrices números reales
cualesquiera, aunque se podrían tomar elementos de cualquier otro cuerpo o
anillo. La matriz cero es aquélla en la que todos los elementos son 0; la matriz
identidad Im de orden m, es una matriz cuadrada de orden m en la cual todos los elementos son
cero excepto los de la diagonal principal, que son 1. El orden de la matriz
identidad se puede omitir si se sobrentiende con el resto de la expresión, con
lo que Im se escribe
simplemente I.
La suma de dos matrices sólo está definida si ambas
tienen el mismo tamaño. Si A = (aij)
y B = (bij) tienen igual tamaño,
entonces la suma C = A + B
se define como la matriz (cij), en la que cij = aij + bij, es decir, para sumar dos
matrices de igual tamaño basta con sumar los elementos correspondientes. Así,
para las matrices mencionadas anteriormente
![]()
El conjunto de todas las matrices
de un determinado tamaño tiene las propiedades uniforme, asociativa y
conmutativa de la adición. Además hay una matriz única O tal que para cualquier matriz A,
se cumple A + O = O + A = A
y una matriz única B tal que A + B
= B + A = O.
El producto AB de dos matrices, A y B, está definido sólo si el número de
columnas del factor izquierdo, A es igual
al número de filas del factor derecho, B;
si A = (aij) es de tamaño m × n
y B = (bjk) es de tamaño n × p,
el producto AB = C = (cik)
es de tamaño m × p, y cik
está dado por
![]()
es decir, el elemento de la fila i y la columna k del
producto es la suma de los productos de cada uno de los elementos de la fila i del factor izquierdo multiplicado por
el correspondiente elemento de la columna k
del factor derecho.
ÁLGEBRA LINEAL
El concepto geométrico de vector como segmento
rectilíneo de longitud, dirección y sentido dados, puede generalizarse como se
muestra a continuación. Un n-vector (vector n-dimensional, vector de orden n o vector de longitud n)
es un conjunto ordenado de n
elementos de un cuerpo. Al igual que en la teoría de matrices, los elementos de
un vector pueden ser números reales. Un n-vector v se
representa como
v = (x1, x2, ..., xn)
Las líneas de una matriz son vectores: las
horizontales son vectores fila y las verticales vectores columna. Las x se denominan componentes del vector.
La suma de vectores (de igual
longitud) y la multiplicación por un escalar se definen de igual manera que
para las matrices, y cumplen las mismas propiedades. Si
w = (y1, y2, ..., yn)
y k
es un escalar (número real), entonces
v + w = (x1 + y1,
x2 + y2, ..., xn
+ yn)
y
kv = (kx1,
kx2,
..., kxn)
Si k1, k2,
..., km son escalares, y v1, v2, ..., vm son n-vectores, el n-vector
v = k1v1 + k2v2 + ... + kmvm
se denomina combinación lineal de los vectores
v1, v2, ..., vm. Los m n-vectores
son linealmente independientes si la única combinación lineal igual al n-vector cero, 0 = (0,0, ..., 0), es aquélla en que k1 = k2 = ... = km
= 0. Si existe otra combinación lineal que cumple esto, los vectores son
linealmente dependientes. Por ejemplo, si v1
= (0, 1, 2, 3), v2 = (1,
2, 3, 4), v3 = (2, 2, 4,
4) y v4 = (3, 4, 7, 8),
entonces v1, v2 y v3 son linealmente independientes, pues k1v1 + k2v2 + k3v3
= 0 si y sólo si k1 = k2 = k3 = 0; v2,
v3 y v4 son linealmente dependientes pues v2 + v3 - v4
= 0. Si A es una matriz de rango r, entonces al menos un conjunto
de r vectores fila o columna es un
conjunto linealmente independiente, y todo conjunto con más de r vectores fila o columna es un conjunto
linealmente dependiente.
Un espacio vectorial V es un conjunto no vacío de vectores (véase Teoría de conjuntos) que cumple
las siguientes propiedades: (1) si ve
V y w e V, entonces (v + w) e V, y (2) si v e V y k es un escalar
cualquiera, entonces kv e V. Si S = {vi}
es un conjunto de vectores, todos ellos de la misma longitud, todas las
combinaciones lineales de los vectores v
forman un espacio vectorial V. Se
dice que este espacio vectorial es generado por los v. Si el conjunto B = {w1} genera el mismo espacio
vectorial V, y está formado por
vectores linealmente independientes, se dice que B es una base de V. Si
una base de V contiene m vectores, entonces toda base de V contiene exactamente m vectores, y se dice que V es un espacio vectorial de dimensión m. Los espacios euclídeos
de dos y tres dimensiones se pueden representar por parejas y tríos ordenados
de números reales. Las matrices se pueden utilizar para describir
transformaciones lineales de un espacio vectorial a otro.
Para
entrar una matriz a tu TI-89
Para crear una matriz
cualquiera llamada A o el nombre que usted desee:

Presione la tecla:
![]()
Escoja:
![]()
Luego Escoja:
![]()
![]()
Para colocar texto:
Para un folder, escoja:
![]()
A menos que haya creado
otro folder en donde guardar la matriz
![]()
Cuando este llenando los encasillados en blanco, use los cursores de dirección para moverse sobre los mismos. No presione
a menos que este seguro
que toda la información es correcta.
![]()
En variables escriba el nombre de su matriz utilizando:
![]()
Escriba el # de filas (3), en este caso, y el # de columnas (4), en este
caso. Luego presione:
![]()
Para colocar las entradas de la matriz en la calculadora, presione :
Luego de cada entrada.
Use los cursores de flechas para moverse entre las
filas y las columnas y editar las entradas.
![]()
![]()
Presione
cuando haya terminado de
entrar su matriz.
![]()
Presione
![]()
y el nombre que le dió a su matriz, presione
para que su matriz
aparezca en la pantalla.
Resolviendo un sistema de ecuaciones
Para
resolver un sistema de ecuaciones, entramos el sistema como si fuera una matriz
en nuestra calculadora y luego colocamos la matriz en "reduced row echelon form (rref)",
por sus siglas en inglés. Cuando se utiliza la opción rref
la calculadora utiliza una versión del método de eliminación para resolver el
sistema dado.
Por ejemplo para
resolver el siguiente sistema de ecuaciones:
X1
- 2 X2 + X3 = 0
2 X2 - 8 X3 = 8
-4 X1 + 5 X2 + 9
X3 = -9
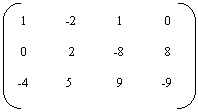
Entre la matriz: con
el nombre dado por usted.
Haga que la calculadora
ponga la matriz en reduced row
echelon form:
![]()
![]()
![]()
![]()
Presionando
y luego escriba el
nombre de su matriz seguido por )

Su calculadora devolverá la siguiente matriz:
Reescriba esta matriz de nuevo como un sistema de ecuaciones:
1X1 + 0X2 + 0X3 = 29
0X1 + 1X2 +
0X3 = 16
0X1 + 0X2 + 1X3= 3
En otras palabras:
X1 = 29
X2 = 16
X3 = 3
Lo cual significa que su
sistema esta resuelto.