Criterio de Routh-Hurwitz
Dado ![]() ,
donde
,
donde ![]() es la ecuación característica de algún sistema.
es la ecuación característica de algún sistema.
I. Método de Routh
Para que todos los polos estén en el semiplano izquierdo es necesario que
A. Las ![]()
B. Todos los determinantes, ![]() , deben ser positivos. Donde
, deben ser positivos. Donde ![]() se definen de las matrices
formadas del siguiente arreglo:
se definen de las matrices
formadas del siguiente arreglo:
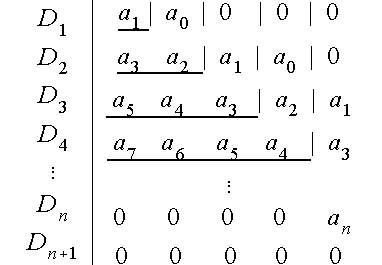 Note que
Note que ![]() es cero, por tener una fila de cero, y por lo tanto el arreglo acaba con
es cero, por tener una fila de cero, y por lo tanto el arreglo acaba con ![]() .
.
Ejemplo 1: Dada la ecuación característica , ![]() determinar si el
sistema es estable o no.
determinar si el
sistema es estable o no.
Solución:
Primero observamos que los coeficientes de la ecuación característica son todos
positivos. Luego, construimos la matriz para determinar los determinantes.
De aquí caculamos los determinantes:
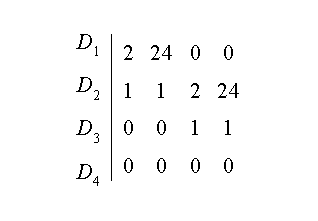
![]()
![]()
![]()
Esto nos dice que el sistema es inestable.
![]() (No es necesario calcularlo, por la fila
de ceros al final de la matriz.)
(No es necesario calcularlo, por la fila
de ceros al final de la matriz.)
I. Método de Routh-Hurwitz
Si las ![]() se cumple, entonces el número de polos en el
semiplano derecho es igual al número de cambios en signo de los coeficientes de la primera
columna del siguiente arreglo:
se cumple, entonces el número de polos en el
semiplano derecho es igual al número de cambios en signo de los coeficientes de la primera
columna del siguiente arreglo:
 donde
donde
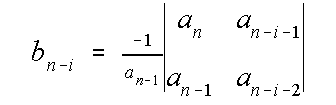 ,
,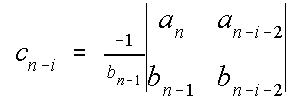 , y así sucesivamente.
, y así sucesivamente.
Teorema de división en una fila:
Los coeficientes de cualquier fila se pueden multiplicar o dividir por un número positivo
sin alterar los cambios en signo de la primera columna.
Ejemplo 2: Determinar cuantas raíces tiene el siguiente polinomio en el semiplano derecho:
![]() .
.
Solución:
Construyendo la siguiente tabla de Routh-Hurwitz podemos ver que hay dos cambios de signo. Por lo tanto, el polinomio tiene dos raíces en el semiplano derecho.
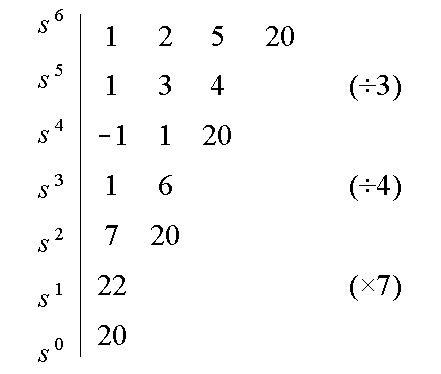 Casos especiales:
Casos especiales:
I. Existe un cero en la primera columna de la tabla de Routh-Hurwitz y un valor diferente de
cero en la misma fila. Esto implica que va haber una división por cero, lo cual está
indefinido.
A. Formas de resolver el problema.
Multiplica el polinomio por (s + 1) y utiliza el método de Routh-Hurwitz sobre el polinomio resultante. Note que los cambios en signo no se afectan.
Sustituir s por 1/x y resolver Routh-Hurwtiz para el nuevo polinomio en x. Esto
equivale a invertir los coeficientes de
![]() ; es decir
; es decir
![]() .
.
Reemplazar el cero de la primera columna por un número![]() .
. ![]() Es
infinitesimalmente positivo, y por lo tanto diferente de cero. Al menos los cambios
en signo se preservan.
Es
infinitesimalmente positivo, y por lo tanto diferente de cero. Al menos los cambios
en signo se preservan.
II. Resulta una fila de ceros en la tabla de Routh-Hurwitz.
A. Implicaciones
Existe una ecuación auxiliar, ![]() , que sale de los coeficientes de la fila anterior.
, que sale de los coeficientes de la fila anterior.
Las raíces de ![]() son también raíces de
son también raíces de ![]() , y éstas ocurren en pares de
singularidad simétrica con el origen.
, y éstas ocurren en pares de
singularidad simétrica con el origen.
Ejemplo 3: Hallar las raices del siguiente polinomio usando Routh-Hurwitz:
![]()
Solución:
Construyendo la siguiente tabla de Routh-Hurwitz podemos ver que existe una fila de ceros.
 De la fila anterior podemos sacar la siguiente
ecuación auxiliar:
De la fila anterior podemos sacar la siguiente
ecuación auxiliar: ![]()
De A(s) tenemos que dos raices son
![]()
Ahora dividiendo el polinomio original por A(s) obtenemos la siguiente ecuación:
![]()
Utilizando la fórmula cuadrática hallamos las dos raices restantes: ![]()